Como Fazer Pitagoras
Teorema de Pitágoras… Imagina só, essa expressão pode até soar complicada, mas fica tranquila! Ele é um super aliado na matemática e no dia a dia. Se você sempre se perguntou como dominar essa ferramenta, chegou a hora de desvendar todos os segredos de como fazer Pitágoras de um jeito fácil e divertido.
O que é o Teorema de Pitágoras?
O Teorema de Pitágoras é uma relação matemática entre os lados de um triângulo retângulo. Em outras palavras, ele nos ajuda a encontrar o comprimento de um lado desse triângulo quando conhecemos os outros dois. A fórmula principal é: a² + b² = c², onde ‘a’ e ‘b’ são os catetos (lados menores) e ‘c’ é a hipotenusa (lado maior, oposto ao ângulo reto).
Vamos combinar, esse teorema é fundamental em diversas áreas, desde a construção civil até a navegação. Pois é, com ele, podemos calcular distâncias, alturas e muitas outras medidas importantes.
A História por Trás do Teorema

Apesar de levar o nome de Pitágoras, um famoso filósofo e matemático grego, estudiosos indicam que o teorema já era conhecido por outros povos, como os babilônios e os egípcios. Contudo, foi Pitágoras quem o demonstrou formalmente, tornando-o uma base fundamental da geometria.
Entendendo os Componentes do Triângulo Retângulo
Antes de tudo, para aplicar o Teorema de Pitágoras, você precisa identificar os catetos e a hipotenusa no triângulo retângulo. Os catetos são os lados que formam o ângulo reto (90º), enquanto a hipotenusa é o lado oposto a esse ângulo, sendo sempre o maior lado do triângulo.
A Fórmula Mágica: a² + b² = c²
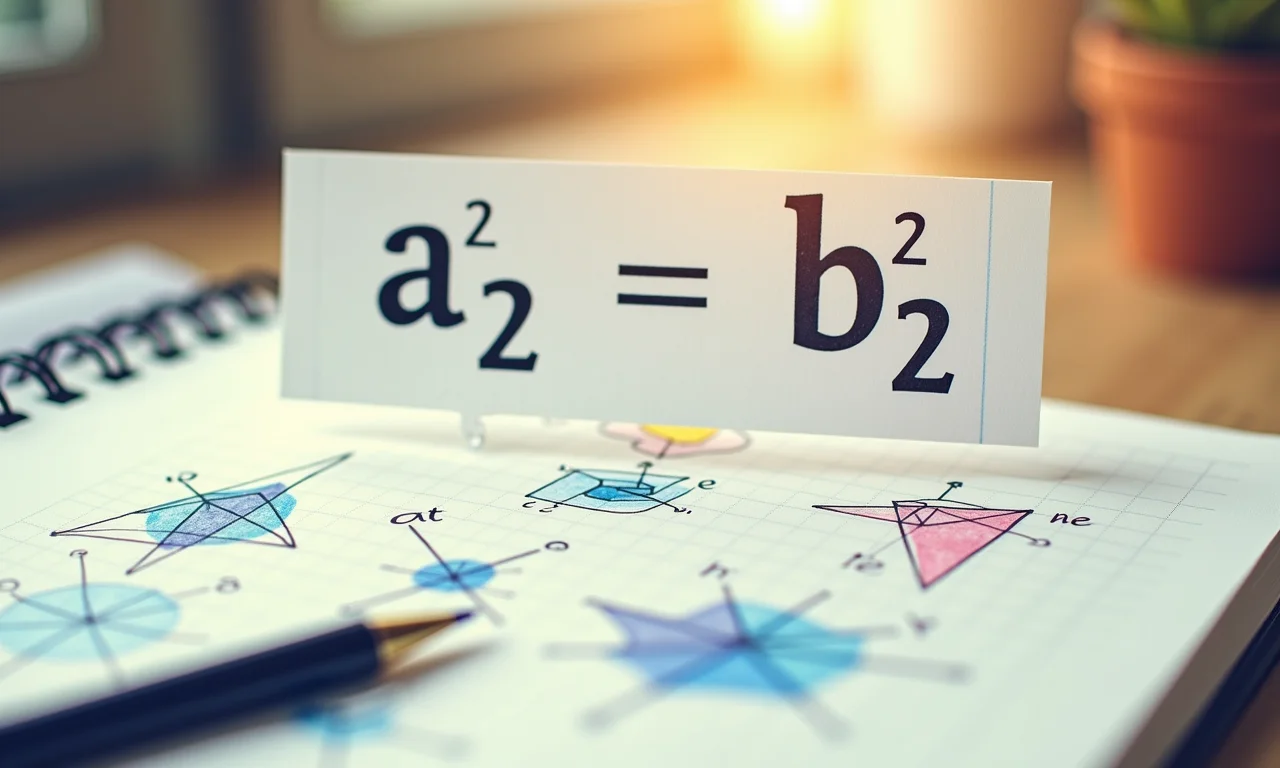
Essa fórmula é a chave para resolver qualquer problema envolvendo o Teorema de Pitágoras. ‘a’ e ‘b’ representam os comprimentos dos catetos, e ‘c’ representa o comprimento da hipotenusa. Elevando cada um ao quadrado e somando os catetos, obtemos o quadrado da hipotenusa. Imagine, é como se estivéssemos montando um quebra-cabeça matemático!
Passo a Passo: Calculando a Hipotenusa
Se você conhece os valores dos catetos e precisa encontrar a hipotenusa, basta substituir os valores na fórmula e resolver a equação. Veja um exemplo: se a = 3 e b = 4, então c² = 3² + 4² = 9 + 16 = 25. Logo, c = √25 = 5. Simples, né?
Encontrando um Cateto Desconhecido

E se você souber o valor da hipotenusa e de um dos catetos? Sem problemas! Basta rearranjar a fórmula. Por exemplo, se você conhece ‘c’ e ‘a’, para encontrar ‘b’, a fórmula seria: b² = c² – a². Aí é só substituir os valores e resolver a equação. Fica tranquila, com a prática, isso se torna automático!
Exemplo Prático: Uma Escada Encostada na Parede

Vamos imaginar uma situação real: uma escada de 5 metros está encostada em uma parede. A base da escada está a 3 metros da parede. Qual a altura que a escada alcança na parede? Aqui, a escada é a hipotenusa (c = 5), a distância da base até a parede é um cateto (a = 3), e a altura que queremos encontrar é o outro cateto (b). Aplicando a fórmula: b² = 5² – 3² = 25 – 9 = 16. Logo, b = √16 = 4 metros. Viu só como o Teorema de Pitágoras pode ser útil?
Usando o Teorema de Pitágoras no Dia a Dia

Pois é, o Teorema de Pitágoras não serve só para resolver exercícios de matemática. Ele pode ser usado em diversas situações cotidianas, como calcular a diagonal de um terreno retangular, verificar se um canto está realmente em ângulo reto, ou até mesmo para planejar a distribuição de móveis em um cômodo.
Dicas Extras para Dominar o Teorema
- Desenhe o triângulo: Visualizar o problema ajuda muito!
- Identifique os lados: Tenha certeza de qual é a hipotenusa e quais são os catetos.
- Pratique: Quanto mais você resolver exercícios, mais fácil ficará.
Recursos Online para Praticar
Para te ajudar a praticar, existem diversos sites e aplicativos que oferecem exercícios e exemplos resolvidos do Teorema de Pitágoras. Alguns exemplos são o Brasil Escola e o Só Matemática. Além disso, muitos vídeos no YouTube explicam o teorema de forma didática e divertida. Aproveite esses recursos para aprimorar seus conhecimentos!
Aplicações Avançadas do Teorema

O Teorema de Pitágoras também é fundamental em áreas mais avançadas da matemática e da física. Ele é usado, por exemplo, no cálculo de vetores, na trigonometria e na geometria analítica. Entender bem esse teorema é um passo importante para quem deseja seguir carreira nessas áreas.
| Conceito | Definição | Fórmula |
|---|---|---|
| Hipotenusa | Lado oposto ao ângulo reto | c |
| Catetos | Lados que formam o ângulo reto | a e b |
| Teorema de Pitágoras | Relação entre os lados de um triângulo retângulo | a² + b² = c² |
Dúvidas Frequentes
O Teorema de Pitágoras funciona em qualquer triângulo?
Não, ele só funciona em triângulos retângulos, que possuem um ângulo de 90 graus. Pois é, se o triângulo não for retângulo, você precisará usar outras ferramentas matemáticas.
Como saber qual lado é a hipotenusa?
A hipotenusa é sempre o lado oposto ao ângulo reto e é o maior lado do triângulo. Imagina!, é só identificar o ângulo de 90 graus e olhar para o lado oposto.
Posso usar calculadora para resolver os cálculos?

Claro! A calculadora pode ser uma grande aliada, principalmente para encontrar raízes quadradas. Só que, tente resolver os exercícios manualmente também, para praticar e entender melhor o teorema.
O Teorema de Pitágoras é usado em outras áreas além da matemática?

Sim! Ele é usado na física, na engenharia, na arquitetura e em muitas outras áreas. Pois é, a aplicação desse teorema é bem ampla.
Para não esquecer:
Lembre-se de sempre verificar se o triângulo é retângulo antes de aplicar o Teorema de Pitágoras. Caso contrário, o resultado estará incorreto.
E aí, preparada para desvendar os mistérios dos triângulos retângulos? Espero que este guia te ajude a dominar o Teorema de Pitágoras e a aplicá-lo em diversas situações. Compartilhe suas dúvidas e experiências nos comentários!



